4.4 AVL树

  AVL(Adelson-Velskii and Landis)树是带有平衡条件（balance condition）的二叉查找树。这个平衡条件必须要容易保持，而且必须保证树的深度是Ο（logN）。最简单的想法是要求左右子树具有相同的高度。如图3-15，这种想法不强求树的深度要浅。

图3-15 一棵坏的二叉树，仅要求在根节点平衡是不够的

  另一种平衡条件是要求每个节点都必须有相同高度的左子树和右子树。如果空子树的高度定为-1，那么只有具有2^k-1个节点的理想平衡树满足这个条件。这种平衡条件保证了树的深度小，不过太严格，难以使用，需要放宽条件。

  一棵AVL树是其每个节点的左子树和右子树的高度最多差1的二叉树（空树的高度定义为-1）。图3-16中，左边的树是AVL树，右边的树不是。

图3-16 两棵二叉查找树，只有左边的树是AVL树

  大致上讲，一棵AVL树的高度最多是1.44log(N+2)-1.328，实际上只比log(N)稍微多一些。图3-17显示了一棵只有最少节点（143）高度为9的AVL树。这棵树的左子树是高度为7且节点数最少的AVL树，右子树是高度为8且节点数最少的AVL树。即，高度为h的AVL树中，最少节点树S（h）由S(h)=S(h-1)+S(h-2)+1给出。函数S(h)与斐波那契数密切相关。

图3-17 高度为9的最小AVL树

  因此，除去可能的插入外（假设懒惰删除），所有的树操作都可以以时间Ο（logN）执行。当插入破坏AVL树的特性时，我们可以通过旋转（rotation）来恢复。把必须重新平衡的节点叫做α 。由于任意节点最多有两个儿子，因此高度不平衡时，α点的两棵子树的高度差2。因此，这种不平衡可能出现在下面的4中情况中：

1. 对α的左儿子的左子树进行一次插入。

2. 对α的左儿子的右子树进行一次插入。

3. 对α的右儿子的左子树进行以此插入。

4. 对α的右儿子的右子树进行一次插入。

  情形(1)和(4)是关于α点的镜像对称，而(2)和(3)也是。第一种情况发生在“外边”，通过单旋转（single rotation）来完成调整。而第二种情况是插入发生在“内部”，通过双旋转（double rotation）来处理。

  4.4.1 单旋转

  图3-18显示了单旋转如何调整情形（1）。具体是：在节点X插入以后，节点k2不满足AVL平衡性质，因为它的左子树比右子树深2层。为了恢复平衡，我们把X上移一层，并把Z下移一层。注意，此时实际上超出了AVL性质的要求。为此，重新安排节点以形成一棵等价的树，如3-18第二部分所示：

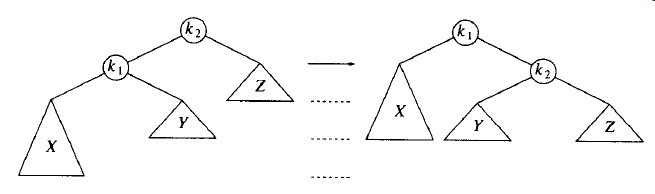
图3-18 单旋转修正情况

  图3-19显示了在将6插入左边原始的AVL树后节点8便不再平衡。于是，我们在7和8之间做一次单旋转，结果得到右边的树。

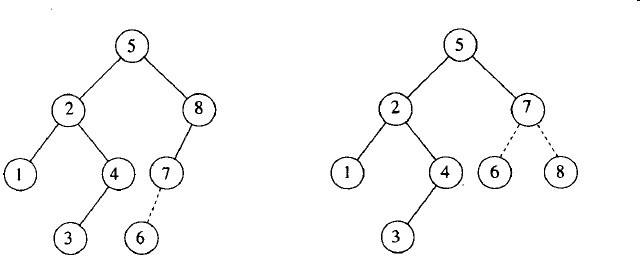
图3-19 插入6破坏了AVL性质，而后经过单旋转又将AVL性质恢复

  情形（4）是一种对称情况，图3-20指出单旋转如何使用：

图3-20 单旋转修正情形（4）

  下面插入4，没问题，但插入5的时候破坏了节点3的AVL性质，通过单旋转调整。除旋转局部引起变化外，树的其余部分也要知晓该变化。如本例中，节点2的右儿子必须重新设置以链接到4而不是3。

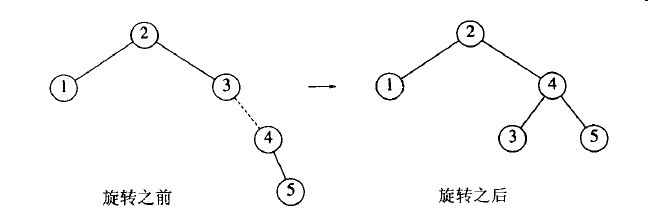
  下面我们插入6。这在根节点产生一个平衡问题。因为它的左子树高度是0而右子树高度为2。因此我们在根处的2和4之间实施一次单旋转。

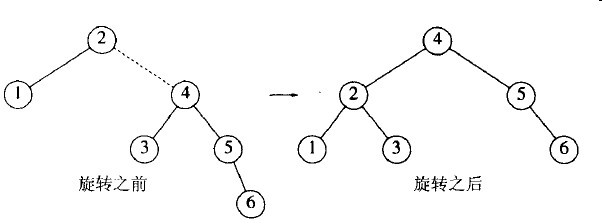
  旋转的结果使得2是4的一个人自而4原来的左子树变成节点2的新的右子树。在该树上的每一项均在2和4之间，因此这个变换是成立的。我们插入的下一项是7，它导致另一次旋转：

 

  4.4.2 双旋转

  上面的算法有个问题：如图3-21所示，它对情形（2）和（3）上面的做法无效。问题在于树Y太深，单旋无法减低它的深度。解决这个问题的双旋转在图3-22中表示出。

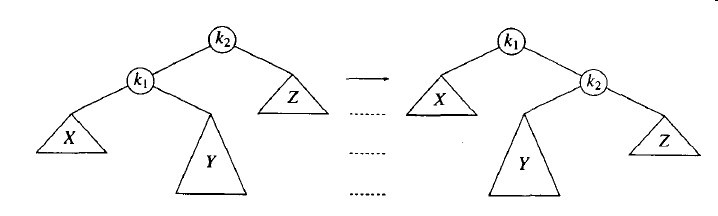
图3-21 单旋不能修正情形（2）

图3-22 左-右双旋转修正情形（2）

  为了重新平衡树。不能再让k3作为根了，而图3-21所示在k3和k1之间又解决不了问题，唯一的选择是把k2作为新根。这迫使k1是k2的左儿子，k3是它的右儿子。从而完全确定了这4棵树的最终位置。最后得到的树满足AVL树的性质。图3-23指出，对称情形（3）也可以通过双旋转得到修正。这两种情形下，其效果与先前在α的儿子和孙子之间旋转而后再在α和它的新儿子之间旋转的效果是相同的。

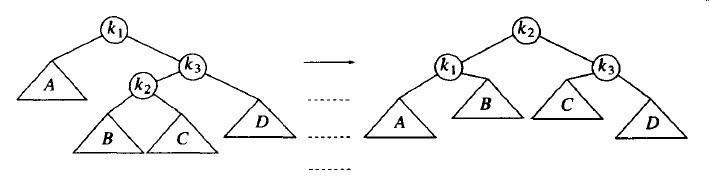
图3-23 右-左双旋转修正情形（3）

  我们继续在前面的例子上倒序插入10-16，接着插入8，然后插入9。插入16很容易，并不破坏平衡的性质，但插入15后引起节点7高度不平衡。这属于情形（3），需要通过一次右-左双旋转来解决。

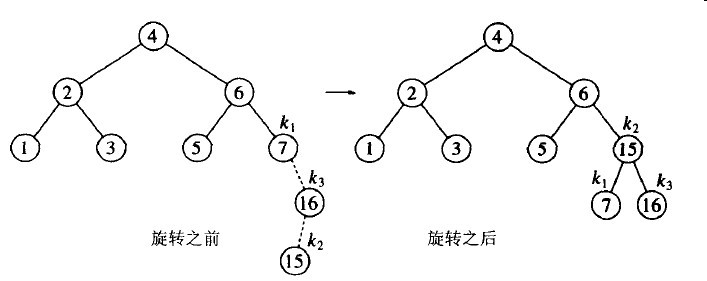
  下面我们插入14，它也需要一个双旋转。此时修正该树的双旋转还是右-左双旋转，它涉及6，15，7。

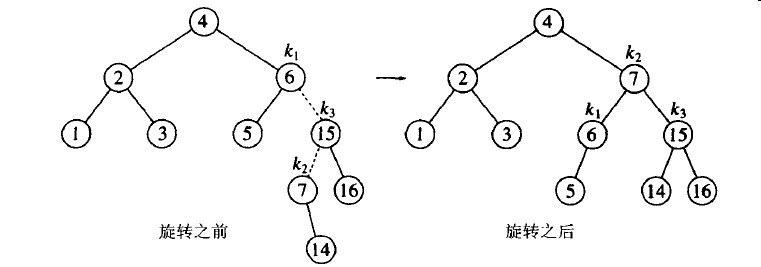
  如果现在插入13，那么在根处就会产生不平衡。由于13不在4和7之间，因此我们直到一次单旋转就可以完成修改任务。

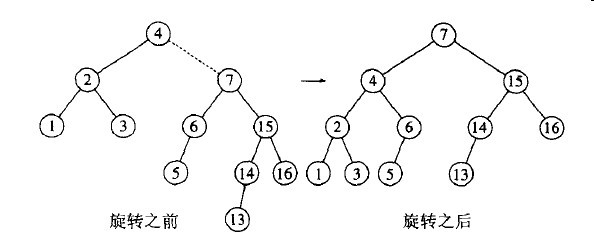
  12也需要一个单旋转：

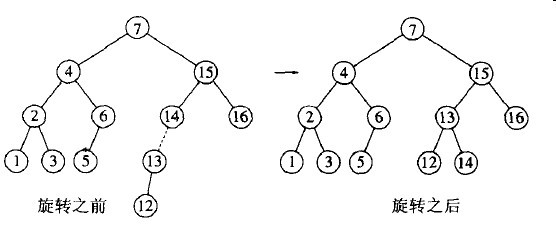
为了插入11，还需要进行一个单旋转，对其后的10的插入也需要这样的旋转。我们插入8而不进行旋转，这样就建立了一棵近乎理想的平衡树。

  最后，插入9以演示双旋转的对称情形。9会引起10节点的不平衡，需要一个双旋转，得到下图：

  现在对上面的讨论做个总结。要将项为X的一个新界点插入到一棵AVL树T中去，我们递归地将X插入到T的相应的子树（称为TLR）。如果TLR的高度不变，那么插入完成。否则，如果在T中出现高度不平衡，那么根据X以及T和TLR中的项做适当的单旋转或双旋转，更新这些高度（并解决好与树的其余部分的链接），从而完成插入。由于编写非递归的程序很困难，所以一般都编写递归程序。

  首先，我们需要AvlNode类

struct AvlNode{  Comparable element;  AvlNode *left;  AvlNode *right;  int height;    AvlNode( const Comparable & theElement, AvlNode *lt, AvlNode *rt,   int h = 0 ) : element( theElement ), left( lt ), right( rt ), height( h )};

  计算AVL节点高度的函数

/** * Return the height of node t or -1 if NULL */ int height( AvlNode *t ) const {   return t == NULL ? -1 : t->height; }

  向AVL树的插入操作

/** * Internal method to insert into a subtree * x is the item to insert * t is the node that roots the subtree * Set the new root of the subtree */ void insert( const Comparable & x, AvlNode * & t ) {   if( t == NULL )     t = new AVLNode( x, NULL, NULL );   else if( x < t->element )   {     insert( x, t->left );     if( height( t->left ) - height( t > right ) == 2 )       if( x < t->left->element )         rotateWithLeftChild( t );       else         doubleWithLeftChild( t );   }   else if( t->element < x )   {     insert( x, t->right );     if( height( t->right() ) - height( t > left ) == 2 )       if( t->right->element < x )         rotateWithRightChild( t );       else         doubleWithRightChild( t );   }   else     ;  //Dupliacate ;do nothing   t->height = max( height( t->left ), height( t->right ) ) + 1 ; }

  对于图3-24中的树，函数rotateWithRightChild把左边的树变成了右边的树，并返回指向新根的指针。函数rotateWithRightChild是对称的。

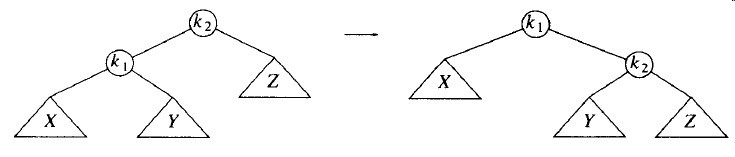
图3-24 单旋转

  代码如下：

/** * Rotate binary tree node with left child * For AVL trees,this is a single rotation for case 1 * Update heights,then set new root */ void rotateWithLeftChild( AvlNode * & k2 ) {   AvlNode *k1 = k2->left;   k2->left = k1->right;   k1->right = k2;   k2->height = max( height( k2->left ), height( k2->right ) ) + 1;   k1->height = max( height( k1->left ), k2->height ) + 1;   k2 = k1; }

  下面是完成图3-25所描述的双旋转的代码：

图3-25 双旋转

/** * Double rotate binary tree node: frist left child * with its right child; then node k3 with the new left child * For AVL trees,this is a double rotation for case 2 * Update heights,then set new root */ void doubleWithLeftChild( AvlNode * & k3 ) {   rotateWithRightChild( k3->left );   rotateWithRightChild( k3 ); }

 

 4.5 伸展树

  本节描述一种相对简单的数据结构，叫伸展树（splay tree），它保证从空树开始任意连续M次对树的操作最多花费Ο（MlogN）时间。一般来说，当M次操作的序列总的最坏情况运行时间为Ο（Mf(N)）时，我们说它是摊还（amortized）运行时间为Ο（f(N)）。因此，一棵伸展树每次操作的摊还代价是Ο（logN）。

  伸展树是基于这样的事实：对于二叉查找树来说，每次操作最坏情况时间Ο（N）并非不好，只要它相对不常发生就行。如果任意特定操作可以有最坏时间界Ο（N），而我们仍然要求一个Ο（logN）的摊还时间界，那么很清楚，只要有一个节点被访问，它就必须被移动。否则，M次访问的时间为Ο（MN）。

  伸展树的基本想法是，当一个节点被访问后，它要经过一系列AVL树的旋转被推到根上。

 

  4.5.1 一个简单的想法（不能直接使用）

  实施上面的描述的重新构造的一种方法是执行单旋转，自底向上进行。这意味着将对访问路径上的每一个节点和它们的父节点实施旋转。考虑下面的树中对k1进行一次访问（一次find）之后发生的情况。

  虚线是访问的路径。首先，在k1和它的父亲节点之间实施一次单旋转，得到下面的树。

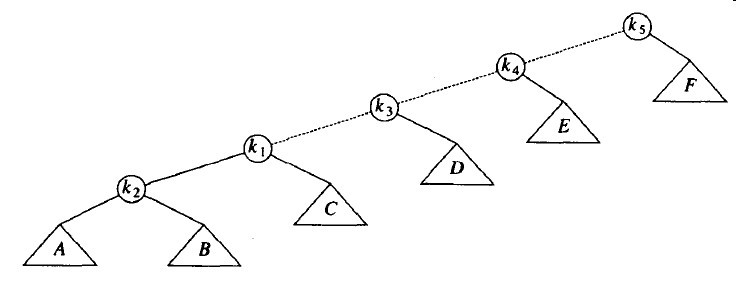
  然后，在k1和k2之间旋转，得到下一棵树。

  再实行两次旋转直到k1到达树根。

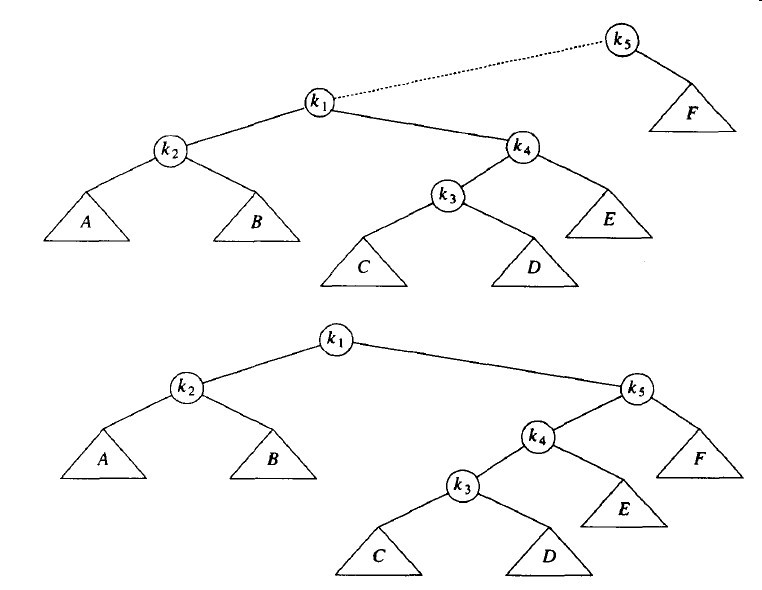
  这些旋转的效果是将k1一直推向树根，使得对k1的进一步访问很容易（暂时的）。不足的是它把另外的一个节点（k3）几乎推向了和k1同样的深度。事实证明，使用这种策略将会存在一系列M个操作共需要Ω(MN)的时间。

 

  4.5.2 伸展

  伸展（splaying）的方法类似于上面的方法，不过在如何旋转上稍微有些选择的余地。我们仍是自底向上沿着访问路径旋转。令X是在访问路径上的一个（非根）节点，我们将在这个路径上实施旋转操作。如果X的父节点是树根，那么只要旋转X和树根。这就是沿着访问路径的最后旋转。否则，X就有父亲（P）和祖父（G），存在两种情况以及对称的情形要考虑。第一种情况是之字形（zig-zag）情形（见图3-26）。如果这种情况下我们就执行一次AVL那样的双旋转。否则出现另一种一字形（zig-zig）情形：X和P或者都使左儿子，或者都使右儿子。这种情况下，我们把图3-27左边的树换为右边的树。

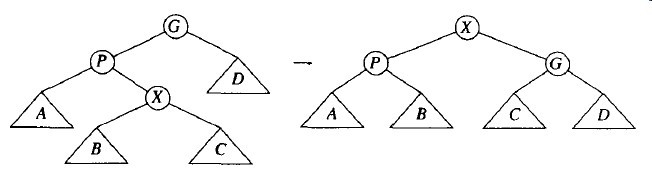
图3-26 之字形情形

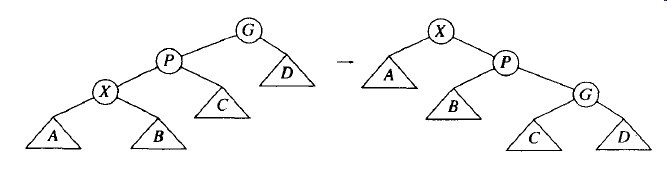
图3-27 一字形情形

  作为例子，考虑来自最后例子中的树，对k1执行一次contains;

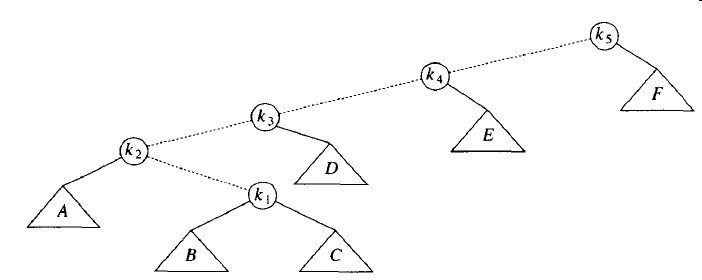
  伸展的第一步是在k1，显然是一个一字形，因此我们用k1、k2和k3执行一次标准的AVL双旋转。得到如下树：

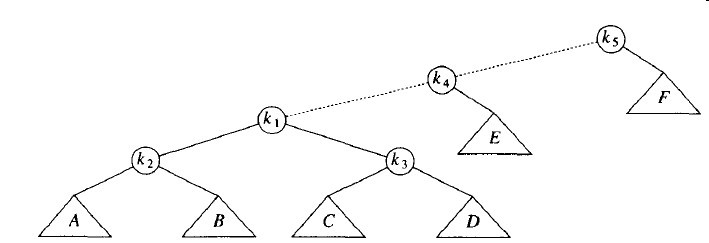
  在k1的下一步伸展是一个一字形，因此我们用k1、k4和k5做一字形旋转，得到最后的树。

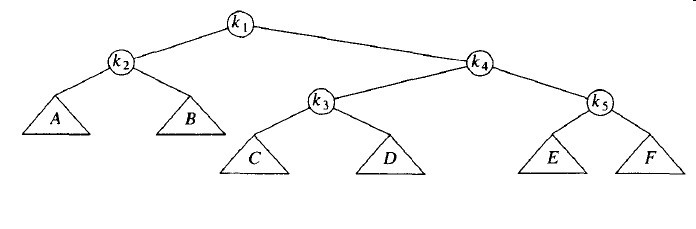
  伸展树操作不仅将访问的节点移动到根处，而且还把访问路径上大部分节点的深度大致减少一半的效果（某些浅的节点最多向下推两个层次）。

  为了看出延伸树与简单旋转的差别，再来考虑1，2，3，…，各项插入到初始空树中去的效果。图3-28指出在项为1的节点进行伸展的结果，区别在于对项2的访问时间只花费了N/2：不存在像以前那么深的节点。

对项2的访问将把这些节点带到距根N/4的深度之内，并且如此进行下去直到深度大约为logN。

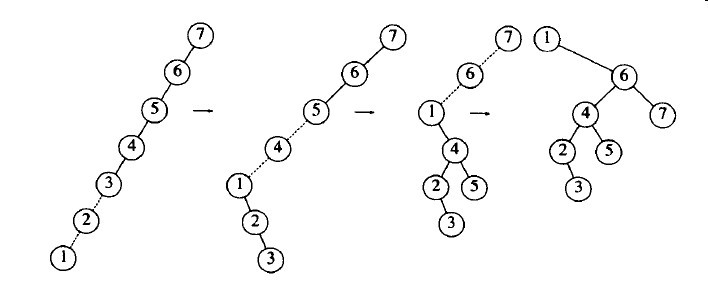
图3-28 在节点1伸展的结果

  图3-29到图3-37显示在32个节点的树中访问项1到9的结果，这棵树最初只含左儿子。伸展树没有简单树旋转策略中常见的低效率的不良现象。

图3-29 将全部由左儿子构成的树在节点1伸展的结果

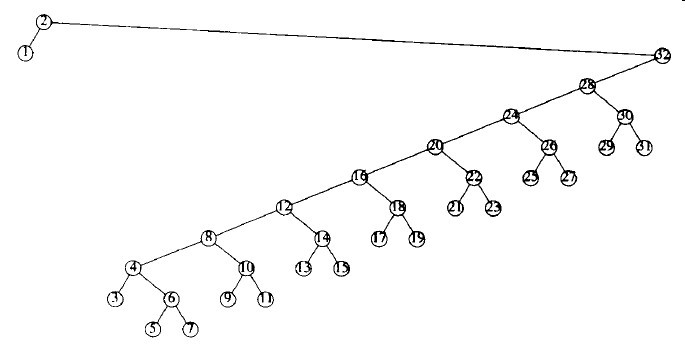
图3-30 将前面的树在节点2伸展的结果

图3-31 将前面的树在节点3伸展的结果

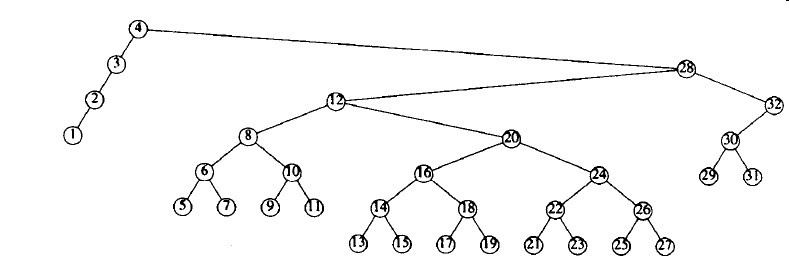
图3-32 将前面的树在节点4伸展的结果

图3-33 将前面的树在节点5伸展的结果

图3-34 将前面的树在节点6伸展的结果

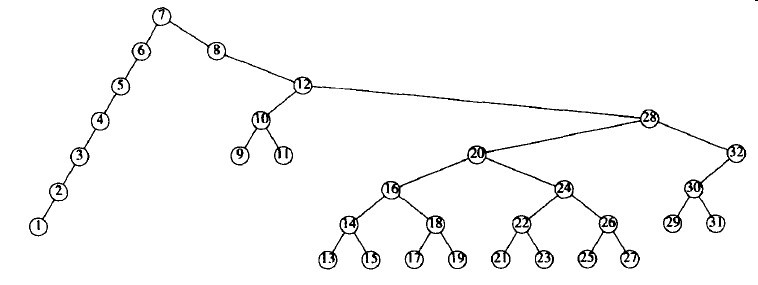
图3-35 将前面的树在节点7伸展的结果

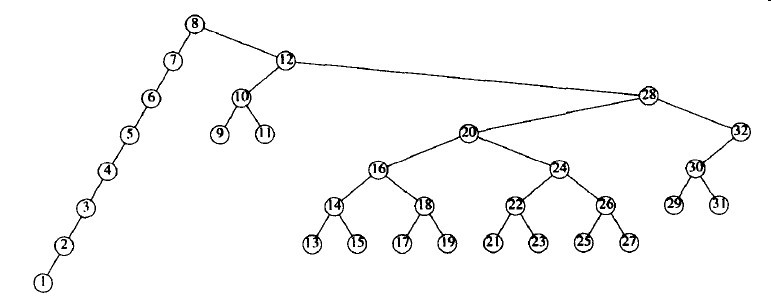
图3-36 将前面的树在节点8伸展的结果

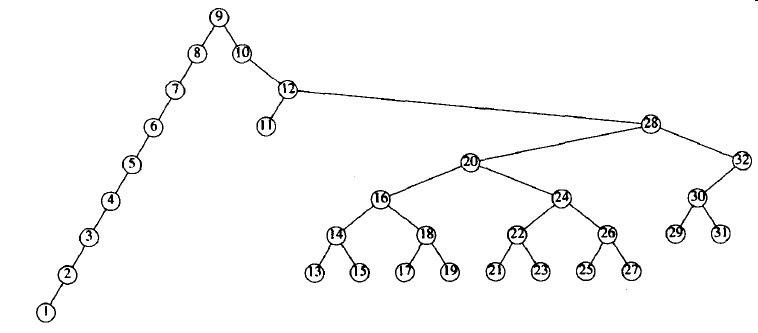
图3-37 将前面的树在节点9伸展的结果

  这些图着重强调了伸展树基本的和关键的性质。当访问路径长而导致超出由正常查找时间的时候，这些旋转树对未来的操作有益。当访问耗时很少时，这些操作反而不那么有益，甚至有害。

 

 4.6 树的遍历

  由于二叉查找树对信息已进行排序，因而按照排序的顺序列出所有的项很简单。下面是递归的方法：

/*** Print the tree contents in sorted order*/void printTree( ostream & out = cout ) const{  if( isEmpty() )    out << " Empty tree " << endl;  else    printTree( root, out );}/** * Internal method to print a subtree rooted at t in sorted order */ void printTree( BinaryNode *t, ostream & out ) const {   if( t != NULL )   {     printTree( t->left, out );     out << t->element << endl;     printTree( t->right, out );   } }

  这类方法当用于树时候则称为中序遍历（inorder traversal）（由于它依序列出了各项，因此是有意义的）。因为在树的每个节点进行处理的工作是常数时间，所以中序遍历的运行时间总是Ο（N）。

  下面是利用后序遍历（postorder traversal），其运行时间也是Ο（N）。

/** * Internal method to compute the height of a subtree rooted at t. */ int height( BinaryNode *t ) {   if( t == NULL )     return -1;   else     return 1 + max( height( t->left ), height( t->right ) ); }

  第三种常用的遍历格式为前序遍历（preorder traversal）。这里，当前节点在其儿子节点之前处理。这种遍历可以用来利用节点深度标志每一个节点。

  第四种遍历用得很少，叫做层序遍历（level-order traversal）。其中所有深度为d的节点要在深度为d+1的节点之前进行处理。与其他遍历不同的是，层序遍历不是在递归实现的：它用到队列， 而不使用递归所默认的栈。

 

 4.7 B树

  迄今为止，我们始终假设可以把整个数据结构储存到计算机的主存中。可是，如果数据太多主存装不下，那么就意味着必须把数据结构放在磁盘上。此时，大Ο模型不再适用，所以寻址规则发生了变化。

  问题在于大Ο分析假设所有的操作都使相等的。然后，现在这个假设就不成立了，特别涉及磁盘I/O操作。磁盘访问的代价太大。不仅如此，处理器的速度还在以比磁盘速度快得多的速度增长（增长相当快的是磁盘的大小）。因此，为了节省一次磁盘访问，我们愿意进行大量的计算。几乎所有的情况下，控制运行时间的都是磁盘访问次数减少一半，那么运行时间也将减少一半。

  不平衡的二叉查找树是非常糟糕的，最坏情形下有线性深度，平均上，一次成功的查找可能需要1.38logN次磁盘访问。在一棵典型的随机构造的树中，我们预料会有一些节点比平均深度深3倍。而AVL树要好一些，典型情形下非常接近logN。

  为了把磁盘访问次数减小到一个非常小的常数，我们愿意写一个复杂的程序来做这件事，因为只要不太冗长，机器指令基本上不占时间。由于典型的AVL树接近最优的高度，因此二叉查找树是不可行的，二叉查找树不能达到logN以下。而解法直觉上看是简单的：如果我们有更多分支，那么我们就有更少的高度。这样，31个节点的理想二叉树有5层，而31个节点5叉树只有3层，如图3-38所示。一棵M叉查找树（M-ary search tree）可以有M路分支。随着分支增加，树的深度减少。一棵完全二叉树的高度大约为log2N，而一棵完全M叉树的高度大约为logMN。

图3-38 31个节点的5叉树只有三层

  在二叉查找树中，我们需要一个键来决定到底取两个分支中的哪个：在M叉查找树中需要M-1个键来决定取哪个分支。为了使这种方案在最坏的情形下有效，需要保证M叉查找树以某种方式得到平衡。否则，像二叉查找树那样，它可能退化为一个链表。

  实现这种想法的一种方法是B树。这里描述的是基本的B树（通常称为B+树）。它有许多变种和改进，但实现起来更复杂，因为考虑的情形太多。不过，容易看出，原则上B树保证只有少数的磁盘访问。

  阶为M的B树是一棵具有下列结构特性的树：

1. 数据项存储在树叶上。

2. 非叶节点存储直到M-1个键，以指示搜索方向：键i代表子树i+1中最小的键。

3. 树的根或者是一片树叶，或者其儿子数在2和M之间。

4. 除根外，所有非树叶节点的儿子数在[M/2]和M之间。

5. 所有的树叶都在相同的深度上并有[L/2]和L之间个数据项，稍后描述L的确定。

  图3-29显示了5阶B树的一个例子。注意，所有非树叶节点的儿子数都在3和5之间（从而有2到4个键），根可能只有两个儿子。这里L=5，因此每片树叶有3到5个数据项。要求节点一半满，将保证B树不致退化为简单的二叉树。B树定义很多，这里只是一种流行的形式。

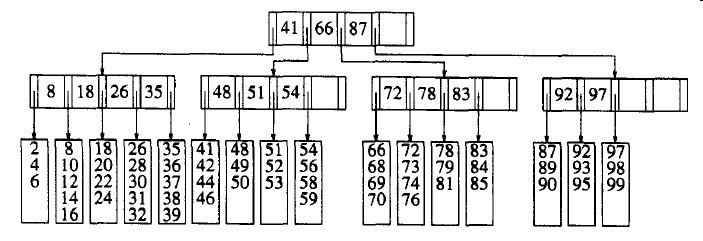
图3-29 5阶B树

  下面的问题是如何向B树添加和删除项。

  我们首先插入。要向3-29中的树插入57。沿树向下查找揭示出它不在树中。此时，把它作为第5个儿子添加到树中。注意可能要为此重新组织该树叶上的所有数据。然而，跟磁盘访问相比（还包含了一次磁盘写），这件事的开销是可以忽略的。

  当然这是相对简单的，因为该树没装满。而这是插入55，要插入其中的那片树叶已经满了。解法并不复杂：由于现在有L+1项，因此把它们分成两片树叶，这两片树叶保证都有所需要的记录的最小个数。对于每次分裂，大致存在L/2次非分裂的插入。

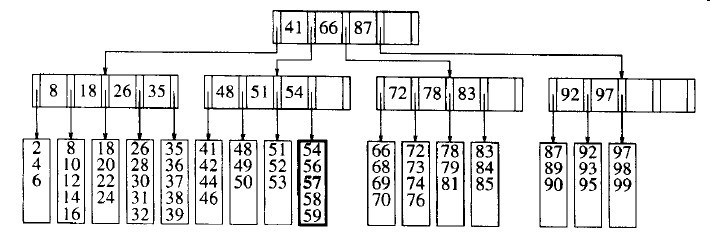
图3-29 将57插入到图3-28的树中后的B树

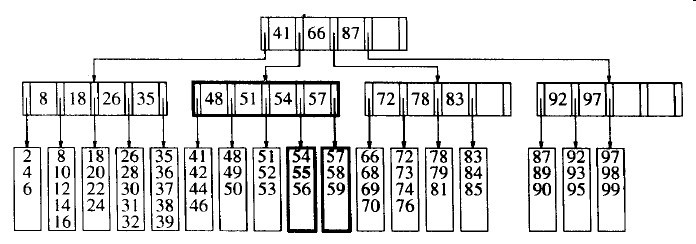
图3-30 将55插入到图3-29的B树中引起分裂成两片树叶

  前面例子中的节点分裂之所以行得通，是因为其父节点的儿子个数尚未满员。如果满员了，例如，将40插入到图3-30的B树中去。父节点会被分裂。

图3-31 把40插入到图3-30的B树中，引起树叶被分裂成两片然后又造成父节点的分裂

  而如果树根也满了，那么唯一的解决方式就是增加B树的高度。但这种情况特别少见。

  可以通过查找要被删除的项并将其删除来执行删除操作。问题在于，如果被删除的项所在的树叶的数据项已经是最小值，那么删除后它的项就低于最小值了。我们可以通过在临节点本身没有达到最小值时领养一个邻项来矫正这种情况。如果临节点也已经是最小值了，那么可以与相邻节点联合以形成一片树叶。可是这意味着其父节点的儿子数低于最小值，那么使用相同的策略继续进行。这个过程可以一直上行至根。

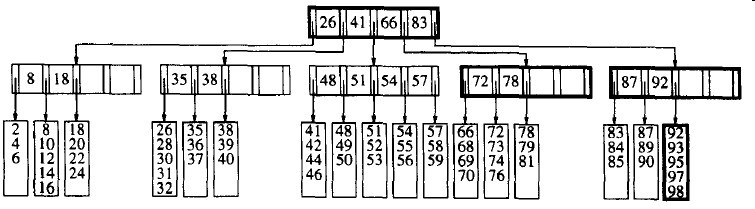
图3-32 从图3-31的B树中删除99后的B树